Describing Motion
Table of contents
- Vocabulary
- Types of Graphs
- Vocabulary + Graphs = Describing Motion
- Activity - Graph Matching
- Activity - Graph Sketching
- Calculation Examples
- Additional Material
Vocabulary
In order to describe motion, we need some to all have the same definitions for a couple of words.
- Position
- Distance
- Speed/Velocity
- Acceleration
- Time
- Change
Position is where something is. Is it over here, is it over there?
Distance is how far. To go from one position to another position is a distance. Measured in meters.
Speed/Velocity is how fast. When you move from one place to the next that takes time. Relating position and time gives you speed. Velocity is just like speed but also has a direction.
Accleration is speeding up or slowing down. When you press on the gas pedal in a car, you accelerate. When you press on the brake, you are also accelerating, it is just negative.
Time is how long.
Summary Table
| Vocabulary | Unit | Description |
|---|---|---|
| Position | – | Where |
| Distance | m (meters) | How far |
| Speed/Velocity | \(\frac{m}{s}\) \(\left(\frac{\text{meter}}{\text{second}}\right)\) | How fast |
| Acceleration | \(\frac{m}{s^2}\) \(\left(\frac{\text{meter}}{\text{second squared}}\right)\) | Speeding up OR slowing down OR changing direction |
| Time | s (second) | How long |
| Change | – | New number |
Types of Graphs
Summary Table
| Shape | Meaning | Picture |
|---|---|---|
| Flat | Constant | 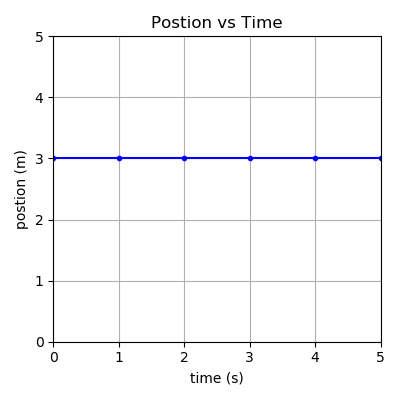 |
| Straight, but not flat | Changing | |
| Curved | Changing-changing |
Vocabulary + Graphs = Describing Motion
Position
Position is where something is. Position is written as a point, just like in math, where the x value is time, and the y value is position, (time, position). An example is (0s, 3m), so when time is 0s, the position is 3m.

Examples
- From your nose to the finger tips of your outstretched hand is 1 meter.
- From Junction City to Ikea in KC is 200 km (there is more about this below).
Velocity
Velocity is both speed and direction - how fast and which way. The units of velocity are meters per second \(\frac{m}{s}\).
To calculate velocity you take the change in position divided by the change in time:
\[\text{Velocity} = \frac{\text{Change in Position}}{\text{Change in Time}} = \frac{\Delta\text{P}}{\Delta\text{t}}\]Examples
- Walking speed is 1\(\frac{m}{s}\)
- The fastest a person can run is about 10\(\frac{m}{s}\)
- A car traveling on the interstate is going 120\(\frac{km}{hr}\) which is about 34\(\frac{m}{s}\)
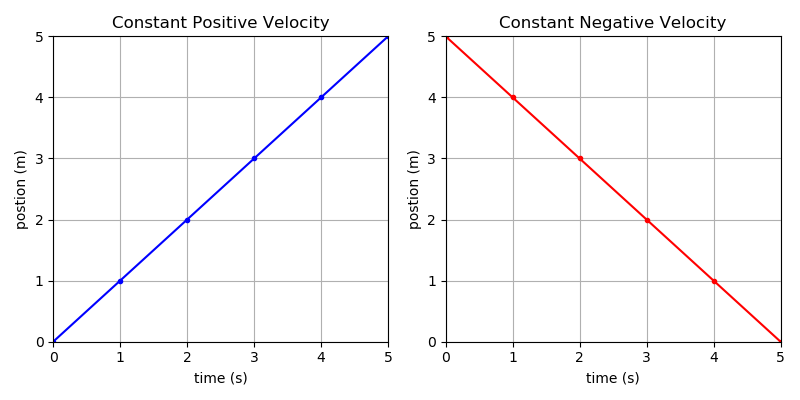
When plotting motion, constant velocity is anytime you have a straight line. If the line is pointed up, then it is a positive velocity. If the line is pointed down, then it is a negative velocity. If the line is flat, then it has no velocity, its position is constant.
Acceleration
Acceleration is change in velocity. Now, since velocity is both speed AND direction, then acceleration can be, change in speed OR change in direction. This means that if I speed up, like when I leave a stop sign in a car, that is accelerating. If I turn a corner, but have a constant speed, then I’m also accelerating.
The units of acceleration are \(\frac{\text{meter}}{\text{second}^2} = \frac{m}{s^2}\).
To calculate acceleration you take the change in velocity divided by the change in time:
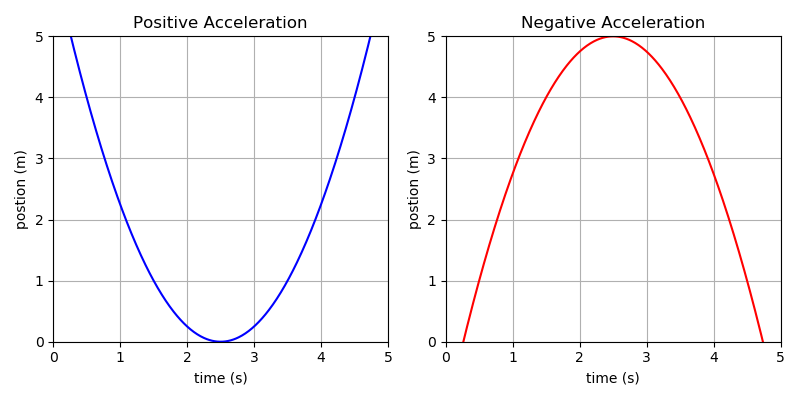
\[\text{Acceleration} = \frac{\text{Change in Velocity}}{\text{Change in Time}} = \frac{\Delta\text{V}}{\Delta\text{t}}\]Note the similarity, position and velocity have the SAME relationship as do velocity and acceleration. This is because one is the slope of the other. Look back at the graphs for velocity, see how they have a constant slope? that means they have a constant velocity.
Now look at the graphs for acceleration. Note, you cannot tell if the acceleration is constant just by looking, you can only tell that it is accelerating. ANY time the position versus time graph is curved, the object is accelerating.
Activity - Graph Matching
Activity - Graph Sketching
Calculation Examples
Additional Material
Units
Motion is described by combinations of length (meters) and time (seconds).
Distance is how far apart two things are and is measured in meters. In math you will learn how to calculate the distance between any two points. For this class we will stick to simple distances.
Speed and velocity both describe how fast something is going and have the units
‘Acceleration’ describes how fast something velocity is changing and has the units:
\[\frac{ \text{meters} }{ \text{seconds squared} } = \frac{m}{s^2}\]Distance
Distance is how far something is. So you have an idea of distances here are some common ones.
- If you stretch out your arm, the distance from your nose to the end of your fingers is 1 meter.
- The width of the nail on your pointer finger is about 1cm.
If an object is moving and you want to track the distance it is covering, you do the following:
\[\text{Distance} = \text{Current Position} - \text{Previous Position}\]This is short handed by using the Greek symbol delta, or $\delta$, which means ‘change in’. Everytime you see the symbol $\delta$ you should immediately replace it with ‘change in’ in your head. Using our new symbol distance becomes:
\[\text{Distance} = \delta\text{Position}\]Look at the picture below. The pen is 13cm long because 18cm - 5cm is 13cm.
Normally we make our lives easier and line the zero up with one side, but that is not always possible.
Vector
A vector is both a distance and a direction, usually represented by an arrow. To explain the difference between direction and a vector, consider my weekend trip.
This weekend I’m going to Ikea in Kansas City. It is 200 km away. If you tell a friend that Kansas City is 200 km away, they have a lot of options.
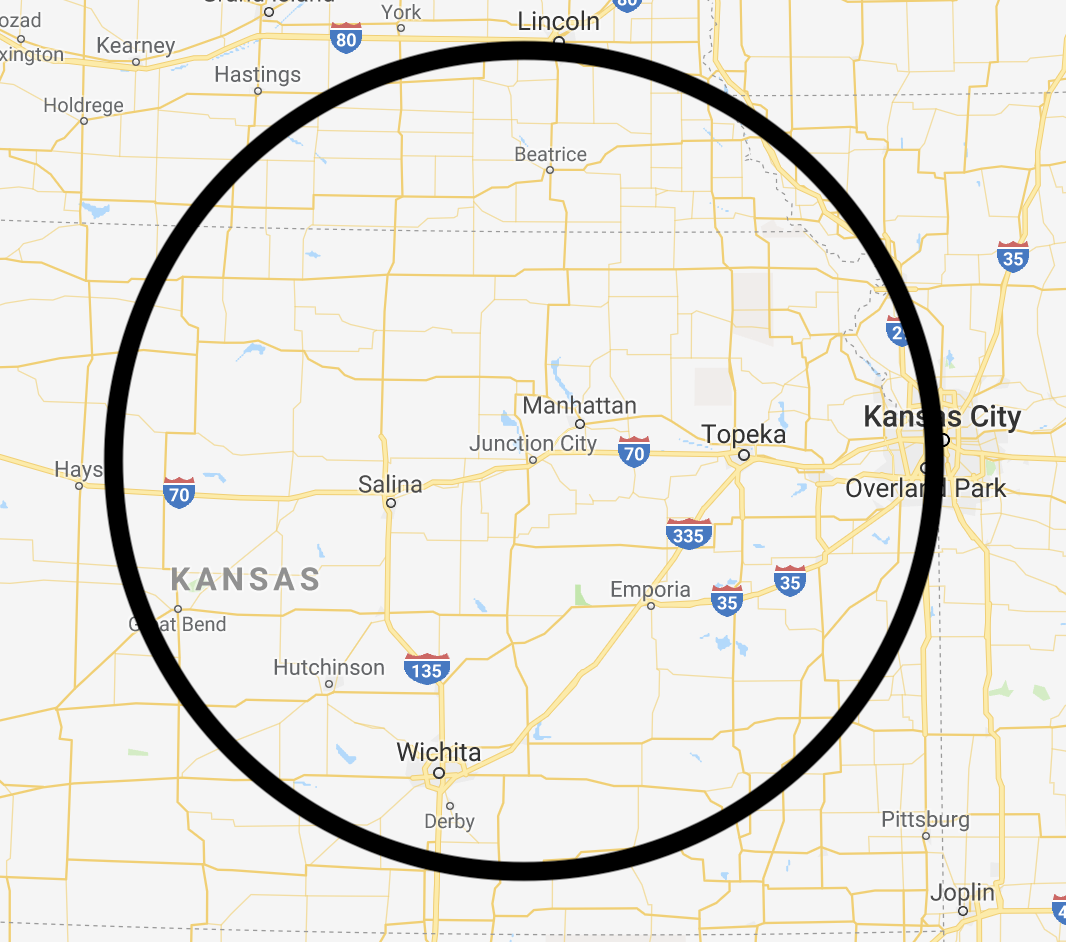
To fix this problem when we say that Kansas City is 200km away, we also have to say in which direction, East.
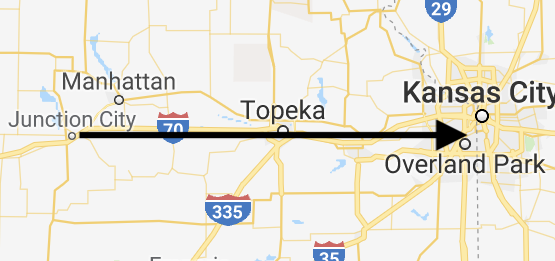
When you specify the direction of a distance it becomes a vector. A vector is simply a direction that also has a direction associated with it.
You can also get vectors using the $\delta$ symbol that we used for distance earlier. But that is is more complicated and will be put at the end for those over-achievers out there.
Speed and Velocity
Speed is just a distance divided by a time. velocity is just a vector divided by time.
A couple of good speeds to remember are:
- Walking speed is about 1 m/s.
- The fastest people can run about 10 m/s.
- Driving down I-70 is 120 km/hr.
Back to my weekend trip. Ikea is 200 km away AND it will take me two hours to get there. To calculate the speed we just need the distance.
\[\text{Speed} = \frac{\text{Distance}}{\text{Time}} = \frac{200 km}{2 hr} = 100\frac{km}{hr}\]But to calcuate the velocity we need a vector, so let’s rephrase where Ikea is. Ikea is 200 km East of Junction City AND it will take me two hours to get there. Now we can calculate the velocity.
\[\text{Velocity} = \frac{\text{Vector}}{\text{Time}} = \frac{200 km East}{2 hr} = 100\frac{km}{hr}\text{ East}\]These are both called average speed, and average velocity. This is because they are the average speed we drove over the whole time. When I go to Kansas City I usually make one stop, so there is a period of time that I’m not moving. The rest of the time I’m usually moving along quite fast, 120 km/hr. When you average out the time I was not moving with the time I was, you get the 100 km/hr that we calculated.
If you want to calculate instantaneous speed and velocity, well check at the end. We’ll talk more about $\delta$ and instantaneous measurments then.
Acceleration
Speed and velocity looked at how a distance or vector changed in time. Acceleration looks at how a speed or velocity changes in time.
The most common acceleration by far is gravity.
- The acceleration due to gravity is 10 $\frac{m}{s^2}$
First let’s look at acceleration as the change in speed divided by the change in time.
\[\text{Acceleration} = \frac{\text{Change in Speed}}{\text{Change in Time}} = \frac{\delta\text{Speed}}{\delta\text{Time}}\]My car is amazing, if I push the gas peddal all the way to the floor when I am headed down the entrance ramp it takes 7.0 seconds to reach 28 m/s (62 mph). That means that the acceleration of my car is:
\[\text{Accleration} = \frac{28 m/s}{7.0 s} = 4 \frac{m}{s^2}\]However, my care is even better at stopping! It only takes 3.3 seconds to stop from 31.3 m/s, so
\[\text{Accleration} = \frac{-31.3 m/s}{3.3 s} = -9.5 \frac{m}{s^2}\]What is the difference between the two answers?
- When accelerating the number was positive
- When slowing down (deccelerating) the number was negative
In physics, if something is getting faster, it has a positive acceleration, if something is getting slower, it has a negative acceleration.
Add
** to do **
- talk about how with velocity there is one other thing, changing direction
- talk about which of the three we can feel.
Position vs Time Graphs
- show examples of position versus time and how to calculate distance, velocity, and acceleration (well you can’t calculate acceleration, but you can recognize when it is happening.)
Instantaneous Velocity and Acceleration
- Explain how the change in can mean a long time, or a short time. The shorter the time, the more instantaneous the velocity is.